|
|
推荐|山东建筑大学2021年山东省成人高考招生简章发表时间:2021-06-16 16:15 学校简介  我校继续教育创办于1958年,当年招收了第一届工业与民用建筑工程专业业余大学本科学员300余人,1979年恢复成人高等学历教育后招收了第一届电大学员80余人,1986年首次招收了本校第一批函授、夜大学员,1992年在原成人教育部的基础上成立了成人教育学院,2010年更名为继续教育学院。在六十多年的发展历程中,学院秉承“团结、敬业、奉献、创新”的办学理念,大力发展继续教育,稳步发展学历教育,积极探索终身教育,务实做好岗位培训,形成了以建设类专业群为主体特色多规格、多层次、多形式的办学体系,为我省建筑业培养了大批的专业技术人才,赢得了社会的广泛赞誉。继续教育学院为学校主管继续教育的二级教学单位,现有教职工17人,在校函授生27000人,每年承担继续教育、岗位培训、社会服务工作等2万人次。 经过多年来的精心培养,我校成人高等教育毕业生受到社会各界肯定,受到教育部、山东省教育厅、山东省住建厅多次表彰,品牌专业建设、特色课程建设在山东省成人教育教学工作中独树一帜,得到了专家的好评。荣获“建设部教育工作先进集体”、“山东省普通高校函授夜大学教育办学水平评估优秀学校”、“山东省成人高等教育品牌专业建设点”、“全国建筑工程专业一级建造师继续教育先进集体”、学校“先进基层党组织”等荣誉称号。 招生简章 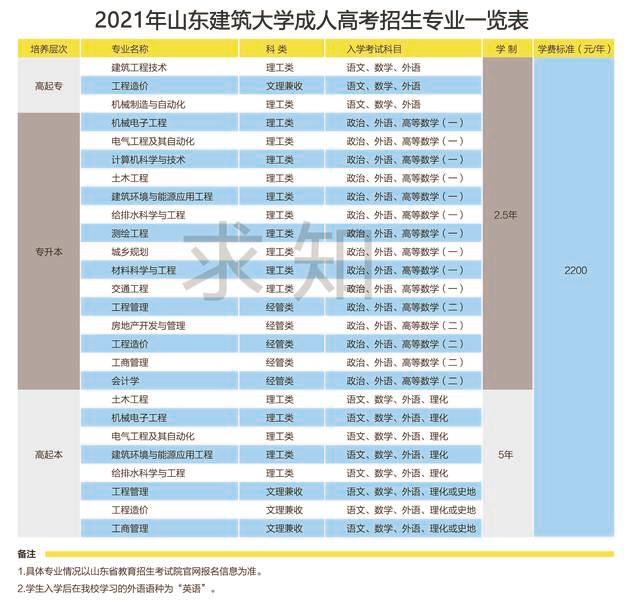 报考条件 1.报考高中起点专科、高中起点本科的考生应具有高中毕业文化程度; 2.报考专科起点本科的考生应具有学信网可查的大学专科及以上毕业文化程度。 报考层次 高中起点升专科(简称高起专) 高中起点升本科(简称高起本) 专科起点升本科(简称专升本) 学制及学习方式 高起专及专升本学制为2.5年,高起本学制为5年。学员可登陆山东交通学院远程教育平台,通过互联网自主学习。  毕业证书和学士学位证书 完成教学计划规定的课程,成绩合格者,颁发相应的本、专科毕业证书,国家承认学历。本科毕业生符合条件的,可申请授予学士学位。本科毕业生符合学位申请条件,并经外语考试合格者可授予学士学位。   求知风采  求知教育,做有温度的继续教育,为您提供定制化的学历提升方案。 服务热线:0531—86912018  |

